Гармонические колебания Вселенной (часть 3)

3.1. Гармония колебаний октавы Веркмейстера

Музыка есть арифметическое упражнение души,

Которая исчисляет себя, не зная об этом.

Г. Лейбниц

Частоты, кратные двум, воспринимаются человеком как один и тот же звук, но в разных тональностях. Это явление называется октавным сходством звуков. Поэтому все гармонические колебания делятся на октавы. В каждой соседней октаве частота звука в два раза ниже (выше), а схожие звуки соответствуют одинаковым нотам.

В современной европейской музыке октава состоит из 12 экспоненциально равных частей от ноты «до» до ноты «си» (3.1). Соотношения их частот близко к отношениям целых чисел, то есть все эти звуки являются гармоническими колебаниями. Такое деление в 1691 г предложил органист Андреас Веркмейстер. Орган обладает уникальной длительностью звука. Поэтому биения (резонансы) частот, прозванные «волками» и характерные для сочетания некоторых нот системы Пифагора, особенно вредили органной музыке. Пифагоров строй позволял музыкантам относительно свободно менять тональность, переводя мелодии на более высокие или низкие частоты, особенно на клавесине, звуки которого быстро затухают.

Сейчас понятно, что нельзя построить многооктавный гармонический ряд колебаний с точными целочисленными соотношениями для всех частот, как это пытались сделать древние музыканты [Брэгг, 1967]. Поэтому целочисленные соотношения, кратные двум, сохраняются между одинаковыми нотами из разных октав, а внутри октавы отношения частот (периодов) только близки к целочисленным соотношениям. Ноты рояля (R), например, описываются последовательностью частот F_R с помощью следующей геометрической прогрессии:

F_R = F₀*2^R/n = 440*2^R/12 Гц, (3.1)

где F₀ = 440 Гц — частота ноты ля 1-й октавы или начальный член геометрической прогрессии (3.1); R — последовательность целых чисел; n= 12 — количество нот в октаве. Частоты рояля изменяются от 27,5 до 4186 Гц, составляя 7 октав. То есть, первая октава расположена в центре клавиатуры и F₀ обозначается как А₄, а самая низкая частота ноты ля соответствует частоте А₀= 27,5 Гц

Музыкантов, определяющих на слух абсолютное значение частоты звука, можно пересчитать по пальцам одной руки. Для музыки более важны правильные соотношения частот, например, гармонические соотношения природного звукоряда — 4:5:6. Чтобы все музыкальные инструменты оркестров звучали согласованно музыканты договорились, чтобы нота А₄ всегда имела частоту 440 Гц. Но решение проблемы для струнных инструментов невозможно расширить на духовые инструменты, так как их звуки могут иметь только точно целочисленные соотношения. Поэтому композиторы и исполнители оркестровой музыки сталкиваются с определенными проблемами, когда в оркестр включены оба типа инструментов.

3.2. Уравнение гармонических колебаний струны

Гармонические звуки от движений струн и их резонансы с древних времен не давали покоя не только музыкантам, их родственникам и соседям, но и ученым — астрономам, физикам и математикам. Возможность теоретического изучения колебаний струны с точки зрения механики появилась только с открытием законов Ньютона (1687) и с разработкой анализа бесконечно малых, интегрального и дифференциального исчислений. Колебания струны изучали Галилей, Декарт, Гюйгенс и многие другие известные ученые. Например, эмпирическая зависимость между частотой, натяжением, площадью поперечного сечения и длиной струны, обнаруженная в 1625 году Мерсенном, была объяснена Тейлором только в 1713 г.

Законы Ньютона позволили начать теоретическое изучение резонансных гармонических колебаний струны. В спор о звучащей струне в XVIII веке оказались вовлечены такие ученые как Д’Аламбер, Эйлер, Д. Бернулли, Лагранж. В результате исследований возникли новые направления в физике и математике. Возможность представления широкого класса функций рядом синусоид и косинусоид, показанная Фурье, ответила на основные вопросы о движении струны. Но проблемы негладкости начальных условий были решены математиками только в середине XX века.

Удар молоточка по струне рояля как раз и создает негладкости начальных условий. Математическим аналогом удара (взрыва) является одномерная (трехмерная) дельта-функция (рис. 3.1). Импульс от удара или δ-функция содержит полный набор частот от нуля до бесконечности. Но колебания, не совпадающие с резонансными, быстро затухают. В результате мы слышим только сумму звуков гармонических резонансных колебаний струны. В этом и состоит основной смысл решения уравнения струны, которая, пока ее не успокоят, генерирует спектр звуковых колебаний, частоты которых выше основного тона в целое число раз.

Увеличение натяжения струны, уменьшение её массы (толщины) и длины увеличивает её максимальную гармоническуюую частоту. Помимо основной стоячей полуволны, равной длине струны, имеется полный набор резонансов на высших гармониках основной частоты f, например, 2f, 3f, 4f, и т. д.

Рис. 3.1. Схематический график одномерной дельта-функции

Эта функция (рис. 3.1) только в точке x=0 обращается в бесконечность, а в остальных точках оси х она равна нулю. Площадь под графиком δ-функцией или её интеграл равен 1. В математических символах сказанное и нарисованное выше записывается гораздо короче:

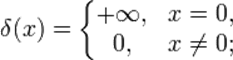
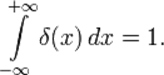
В зарождающемся математическом анализе XVII—XVIII веков присутствовали два основных подхода: наглядный механико-геометрический и формальный алгебраический. Развитие физики и математики тесно связано с изучением гармоник движения струны. Из исследований колебаний струны возникли новые направления в физике и математике, в частности, математическая физика. Изучение уравнения колебаний струны включено в студенческие курсы многих физико-технических специальностей. Математическое понятие дельта-функции аналогично физическим понятиям точечной массы или точечного заряда, когда можно пренебречь размером объекта.

3.3. Законы октав в химии

Джон Ньюлендс

И солнце ярче светит,

И веселей пейзаж,

Когда в желудке плещет

C2 H5 OH

Представления ранних философов об едином атомном строении природы столкнулись с серьезными проблемами по мере открытия всё новых и новых химических элементов. Потом стали обнаруживаться закономерности в их поведении. В частности, подтвердилось учение о гармонии Мира при изучении ритмов химических элементов. Поэтому Д. Ньюлендс в 1866 г расположил элементы по 7 штук в каждом ряду (октаве) в соответствии с их атомными весами (рис. 3.2). Каждый восьмой по порядку элемент в этой таблице частично повторяет свойства первого, как и в природном звукоряде восьмая нота звучит подобно первой (см. рис. 2.1).

Это открытие в современной химии известно под именем закона октавы [Джон Ньюлендс… Википедия]. Д. Ньюлендс первым построил ряды элементов, расположенных в порядке возрастания атомных весов, но выбрал ошибочное число гармоник в октаве, поэтому его закон плохо соответствовал реальности. Слово «октава», происходящее от греческого числительного «восемь», сейчас обозначает любое число звуков с гармонически-закономерным увеличением частоты их колебаний, после которого происходит удвоение частот.

Рис. 3.2.Таблица химических элементов Д. Ньюлендса

[Периодический закон, Википедия]

Д. И. Менделеев

Д. Менделеев долго доказывал своей

супруге, что на первом месте должен

стоять водород, а не семья и дети.

Свою новую таблицу с гармонической октавой из 8-ми элементов, в которой каждый девятый элемент повторяет свойства первого, Д. И. Менделеев публикует только в 1870 г. Им были сделаны очень смелые шаги: он исправил атомные массы урана, тория и других элементов, часть элементов разместил вопреки принятым представлениям об их свойствах, оставил в таблице пустые клетки, для пока не открытых элементов. Его периодический закон, содержаший 10 октав, вскоре получил подтверждение: были открыты предсказанные им галлий, скандий и германий, для которых Менделеев предсказал не только их существование, но и их физические и химические свойства (рис. 3.3).

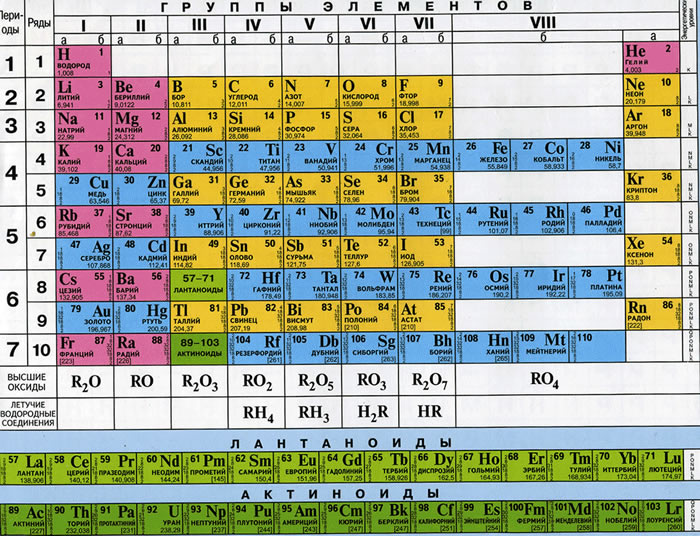
Рис. 3. 3. Таблица химических элементов Д.И. Менделеева

Иллюстрация: edu.glavsprav.ru

После стало понятно, что периодичность химических свойств определяется не атомным весом, а числом электронов в наружных оболочках атомов. Элементы правого столбца группы VIII таблицы (последних нот гармонических октав химии), имеют полностью заполненную электронами внешнюю оболочку атомов, поэтому они отличаются крайне низкой химической активностью. Химические элементы вплоть до урана (содержит 92 протона и 92 электрона) встречаются в природе. Начиная с номера 93 идут искусственные элементы, созданные в лаборатории (рис. 3.3). Пока самый большой заявленный учеными номер — 118.

В группе столбца VIII таблицы Менделеева (Рис. 3.3) сначала каждый элемент ряда (гармонической октавы) увеличивает свой номер и электрический заряд на восемь: гелий, He (2); неон Ne (10); аргон Ar (18); железо Fe (26); из того же IV-го ряда в столбец VIII входит и никель Ni (28); из V-го ряда — криптон (28+8) Kr (36); из VI-го ряда — рутений (36+8) Ru (44) и палладий Pd (46); из VII-го ряда — ксенон (46+8) Xe (54). В следующий ряд VIII входят 9 элементов и лантаноиды (15), поэтому номер и заряд последнего элемента ряда платины Pt (78=54_Xe+24) увеличивается сразу на число кратное восьми (8*3 = 24). Ряд IX завершает элемент радон Rn (86), заряд которого опять на 8 единиц больше заряда платины. В ряд X входят 9 элементов и актиноиды (15), поэтому номер и заряд последнего элемента ряда дармштадтия Ds (110) также увеличивается сразу на число кратное восьми: 86_Rn+24 = 110_Ds. То есть, элементы разных рядов столбца VIII отличаются по заряду на число 8 или кратное ему значение.

Октава таблицы Менделеева состоит из 8 нот в отличие от таблицы Ньюлендса, в которой октава состоит из 7 нот. В слоях (оболочках) атомов химических элементов электроны составляют величины 2, 8, 16 (18) и 32, которые, в основном, могут быть представлены степенями двойки: 1, 3, 4, 5. Гармонические закономерности поведения химических элементов, связанные со степенями двойки, удалось понять благодаря периодической системы Менделеева (рис. 3.3). Однако представления о строении материи сильно усложнились.

Используемые автором количества нот в октаве для классификации земных и солнечных периодов по мере накопления данных и повышения их точности увеличивались вдвое, принимая значения 2, 4, 8, 16 и 32, которые хорошо соответствовали количеству электронов в оболочках атомов. Кроме того, количества нот в гармонических октавах совпадают с размерами куба в пространствах разной размерности (1 ÷ 5): 2¹ — одномерного (длина ребра куба); 2² — двумерного (площадь грани куба); 2³ — объём трехмерного куба; 2⁴ – объём четырехмерного куба и 2⁵ – объём пятимерного куба. Два – это первое целочисленное значение ребра куба, которое позволяет различать размерность по величине объёма куба.

Октава из 64-х нот (2⁶) является, видимо, предельной по точности для природных механизмов формирования периодов (частот) в космических и химических масштабах пространства-времени. В естественных условиях пока не найдено колебаний, соответствующих такой октаве. Косвенным подтверждением этого факта является максимальное число электронов в оболочках химических элементов, соответствующее величине 2⁵. В дальнейшем числа 8, 16 и 32 будут представлять количество нот в гармонических октавах разных природных процессов. Геометрические прогрессии с большим количеством нот в октаве используются для классификации природных периодов, определяемых с большей точностью.

Читайте также:

Гармонические колебания Вселенной (Часть 1)

Гармонические колебания Вселенной (Часть 2)

Гармонические колебания Вселенной (Часть 4)

Гармонические колебания Вселенной (Часть 5)

Гармонические колебания Вселенной (Часть 6)

Борис Берри. Специально для Великой Эпохи