Природа — совершенное творение, убеждаются учёные, которые открывают в строении человеческого тела пропорции золотого сечения, а в головке цветной капусты — фрактальные фигуры.
#img_left#«Изучение и наблюдение природы породило науку», — писал Цицерон в первом столетии до нашей эры. В более поздние времена с развитием науки и отдалением её от изучения природы, учёные с удивлением открывают то, что было известно ещё нашим предкам, но не было подтверждено научными методами.
Интересно находить схожие образования в микро- и макромире, вдохновлять может и то, что геометрию этих образований наука может описать. Кровеносная система, река, молния, ветки деревьев… всё это — схожие системы, состоящие из разных частиц и различные по масштабу.
Пропорции «золотого сечения»
Ещё древние греки, а, возможно, и египтяне, знали пропорцию «золотого сечения». Лука Пачоли, математик эпохи Возрождения, назвал это соотношение «божественной пропорцией». Позже учёные обнаружили, что золотое сечение, которое так приятно глазу человека и которое часто встречается в классической архитектуре, искусстве и даже поэзии, можно повсеместно найти и в природе.
Пропорция золотого сечения — это деление отрезка на две неравные части, в котором короткая часть так относится к длинной, как длинная ко всему отрезку. Отношение длинной части ко всему отрезку — это бесконечное число, иррациональная дробь 0,618…, отношение короткой — соответственно 0,382…
Если построить прямоугольник со сторонами, соотношение которых будет равно пропорции «золотого сечения», и вписать в него ещё один «золотой прямоугольник», в тот — ещё один, и так до бесконечности внутрь и наружу, то по угловым точкам прямоугольников можно провести спираль. Интересно то, что такая спираль совпадёт со срезом раковины наутилуса, а также другими встречающимися в природе спиралями.

Иллюстрация: Homk/wikipedia.org

Окаменелость Наутилуса.
Фото: Studio-Annika/Photos.com

Раковина Наутилуса.
Фото: Chris 73/en.wikipedia.org
Пропорция золотого сечения воспринимается человеческим глазом как красивая, гармоничная. А ещё пропорция 0,618… равняется отношению предыдущего к последующему числу в ряде Фибоначчи. Числа ряда Фибоначчи повсеместно проявляются в природе: это спираль, по которой веточки растений примыкают к стеблю, спираль, по которой вырастают чешуйки на шишке или зёрна на подсолнухе. Что интересно, количество рядов, закручивающихся против часовой стрелки и по часовой стрелке, — это соседние числа в ряде Фибоначчи.
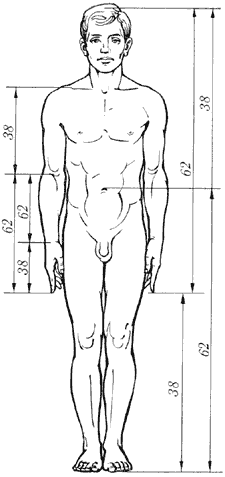
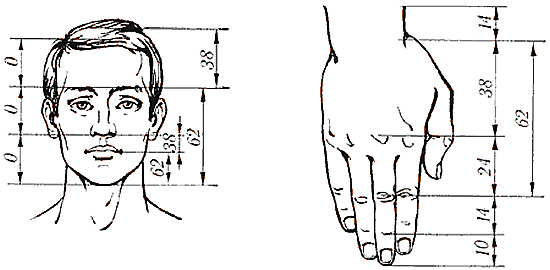
Спирально закручивается головка капусты брокколи и бараний рог… Да и в самом человеческом теле, разумеется, здоровом и нормальных пропорций, встречаются соотношения золотого сечения.
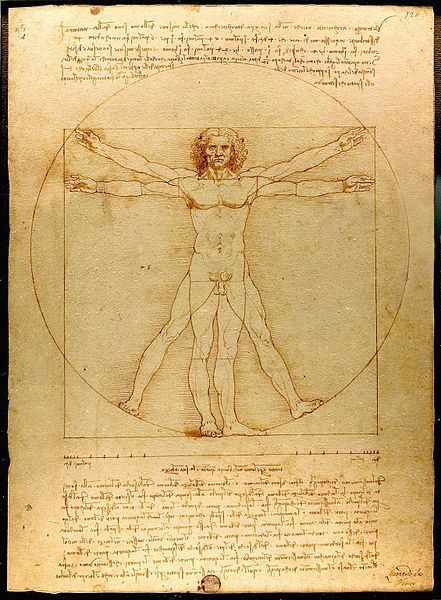
Витрувианский человек. Рисунок Леонардо да Винчи.
1, 1, 2, 3, 5, 8, 13, 21, … — числа ряда Фибоначчи, в котором каждый последующий член получаем из суммы двух предыдущих. Далёкие спиральные галлактики, которые засняли спутники, также закручиваются по спиралям Фибоначчи.

Спиральная галлактика.
Фото: NASA

Три тропических циклона.
Фото: NASA
Двойной спиралью закручена молекула ДНК.

Закрученная спиралью ДНК человека.
Иллюстрация: Zephyris/en.wikipedia.org
Ураган закручивается по спирали, спирально плетёт свою паутину паук.

Паутина паука-крестовика.
Фото: Vincent de Groot/videgro.net
«Золотую пропорцию» можно увидеть и в строении тела бабочки, в отношении грудной и брюшной частей её тельца, а также у стрекозы. Да и большинство яиц вписывается если не в прямоугольник золотого сечения, то в производный от него.

Иллюстрация: Adolphe Millot
Фракталы
Другими интересными фигурами, которые мы можем повсеместно увидеть в природе, являются фракталы. Фракталы — это фигуры, составленные из частей, каждая из которых подобна целой фигуре — не напоминает ли это принцип золотого сечения?
Деревья, молния, бронхи и кровеносная система человека имеют фрактальную форму, идеальными природными иллюстрациями фракталов называют также папоротники и капусту брокколи. «Всё так сложно, всё так просто» устроено в природе, замечают люди, с уважением прислушиваясь к ней.
«Природа наделила человека стремлением к обнаружению истины», — писал Цицерон, словами которого хотелось бы и закончить первую часть статьи о геометрии в природе.
Брокколи — идеальная природная иллюстрация фрактала.
Фото: pdphoto.org
Листья папоротника имеют форму фрактальной фигуры — они самоподобны.
Фото: Stockbyte/Photos.com
Зеленые фракталы: листья папоротника.
Фото: John Foxx/Photos.com
Жилки на пожелтевшем листе, имеющие форму фрактала.
Фото: Diego Barucco/Photos.com
Трещины на камне: фрактал в макро.
Фото: Bob Beale/Photos.com
Разветвления кровеносной системы на ушах кролика.
Фото: Lusoimages/Photos.com

Удар молнии — фрактальная ветка.
Фото: John R. Southern/flickr.com

Веточка артерий в человеческом теле.
Фото: Jupiterimages/Photos.com
Вьющаяся река и её ответвления.
Фото: Jupiterimages/Photos.com
Лёд, замерзший на стекле имеет самоподобный рисунок.
Фото: Schnobby/en.wikipedia.org

Листик плюща с разветвлением прожилок — фракталов по форме.
Фото: Wojciech Plonka/Photos.com